Introduction to Loci

From the point $A\left(0,3\right)$ on the circle $x^2+4x+{\left(y-3\right)}^2=0$, a chord $AB$ is drawn and extended to a point $M$ such that $AM=2AB$. The equation of the locus of $M$ is

The equation of the locus of the points equidistant from the points $A\left(-2,3\right)$ and $B\left(6,-5\right)$ is

A line segment of fixed length $2$ units moves so that its ends are on the positive $x-$axis and on the part of the line $x+y=0$ which lies in the second quadrant. Then, the locus of the mid-point of the line has the equation 

A point $P$ moves so that the sum of squares of its distances from the points $\left(1,2\right)$ and $\left(-2,1\right)$ is $14$. Let $f\left(x,y\right)=0$ be the locus of $P$ which intersects the $x$-axis at the points $A$ and $B$ and the $y-$axis at the points $C$ and $D$. Then the area of the quadrilateral $ABCD$ is equal to

The locus of mid-points of the perpendiculars drawn from points on the line $x=2y$ to the line $x=y$ is

The locus of the mid-point of the portion of a line of constant slope '$m$' between two branches of the rectangular hyperbola $xy=1$ is

The Locus of the point $\left(\tan \theta +\sin \theta , \tan \theta -\sin \theta \right)$ is ($\theta$ isa parameter)

$A\left(0,4\right),B\left(0,-4\right)$ are two points. The locus of $P$ which moves such that $\left|PA-PB\right|=6$ is

If $P$ lies on the line $y=x$ and $Q$ lies on $y=2x$ and $\left|PQ\right|=4$ then the mid point of $PQ$ lies on the curve

A variable line through $A\left(6,8\right)$ meets the curve $x^2+y^2=2$ at $B$ and $C$. $P$ is a point on $BC$ such that $AB,AP,AC$ are in $\mathrm{HP}$. The minimum distance of the origin from the locus of $P$ is

A line segment of length $2l$ sliding with ends on the axes, then the locus of the middle point of the line segment is 

$p,x_1,x_2,\dots ,x_n$ and $q,y_1,y_2,\dots ,y_n$ are two arithmetic progressions with common differences $a$ and $b$ respectively. If $\alpha$ and $\beta$ are the arithmetic means of $x_1,x_2,\cdots ,x_n$ and $y_1,y_2,\cdots ,y_n$ respectively, then the locus of $P\left(\alpha ,\beta \right)$ is

Locus of the centre of rolling circle in a plane will be

Consider a rigid square $ABCD$ as in the figure with $A$ and $B$ on the $X$ and $Y$-axes, respectively.

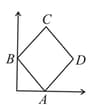
When $A$ and $B$ slide along their respective axes, the locus of $C$ forms a part of

Line PQ is given as $(y+2)=3(x-1)$ Another line AB passes through a point $\left(-5,-6\right)$ and is parallel to PQ. Find the equation of line AB.

The equation of first line is $16x+18y=20$ and the slope of second line is 'q'. if both lines are perpendicular to each other, Then find the value of 'q'

A rod of length$2 l$ slides with its ends on two perpendicular lines, then the locus of its midpoint is

Given points $A(6, 0), B(0, 4)$ and $O$ as the origin, find the locus of a point $P$ such that area of triangle $POB$ is $2$ times the area of triangle $POA.$

For two points $A(2, 1)$ and $B(1, 2), \text{'}P \text{'}$ is a point such that $PA: P B=2:1,$ then locus of $P$ is

The equation of the locus of a point which is equidistant from the points $\left(2,3\right)$ and $\left(4,5\right)$ is: